20世纪60年代发现了资产收益序列的波动聚集性(Volatility Clustering)和厚尾性(Thick Tails),原先的基于最小二乘法同方差假定的传统建模方式失灵。1982年Engle提出的ARCH模型(Autoregressive Conditional Heteroskedasticity 自回归条件异方差模型)属于捕捉金融资产收益序列波动特征模型家族中的佼佼者,并于2003年获诺贝尔经济学奖。
一、LARCH(线性ARCH模型)
1982年Engle最初提出的用于描述英国通货膨胀中存在的条件异方差模型仅仅是线性单变量模型,该模型认为条件异方差是外生变量、滞后的内生变量、时间、参数和前期残差的函数。
基本思想是指在以前信息集下,某一时刻一个扰动项(噪声)的发生是服从正态分布。该正态分布的均值为零,方差是一个随时间变化的量(即为条件异方差),并且这个随时间变化的方差是过去有限项扰动项值平方的线性组合(即为自回归)。
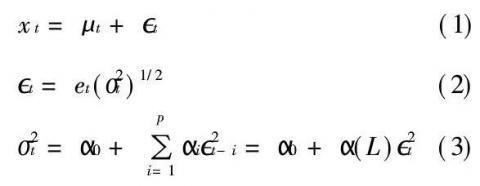
其中扰动项(亦称误差项)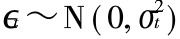 (et是服从标准正态的独立同分布扰动),条件异方差
(et是服从标准正态的独立同分布扰动),条件异方差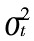 是p期扰动滞后
是p期扰动滞后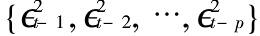 的线性函数。a(L)是滞后算子多项式,为保证
的线性函数。a(L)是滞后算子多项式,为保证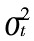 依概率1为正,加了非负约束a0>0,ai>0,i=1,...,p;为保证{xt}的二阶平稳性,要求1-a(L)的根在单位圆外。
依概率1为正,加了非负约束a0>0,ai>0,i=1,...,p;为保证{xt}的二阶平稳性,要求1-a(L)的根在单位圆外。
LARCH的局限性:
1)模型在实际应用中为了获得好的拟合效果,需要很大的阶数p;
2)为简便性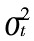 是扰动滞后
是扰动滞后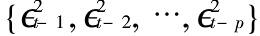 的线性函数,而线性情况只是特例;
的线性函数,而线性情况只是特例;
3)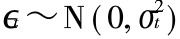 设定为服从正态分布也与一些金融序列实际情况不符,尤其是样本不够大时;
设定为服从正态分布也与一些金融序列实际情况不符,尤其是样本不够大时;
4)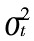 是新息
是新息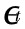 的偶函数,这不太合理,因风险
的偶函数,这不太合理,因风险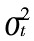 不仅取决于其绝对值大小,其正负同样将有决定作用,即当前收益与未来的波动幅度负相关,例如波动幅度随利差消息(收益低于期望)而增大,随利好消息而降低;
不仅取决于其绝对值大小,其正负同样将有决定作用,即当前收益与未来的波动幅度负相关,例如波动幅度随利差消息(收益低于期望)而增大,随利好消息而降低;
5)ARCH(1)过程具有一步记忆的波动集群性,但确是指数衰减过程,速度很快,与金融市场的某些现象不符,这些现象里在xt的自相关水平普遍较低的情况下,随滞后增大,自相关系数并没有明显彻底的衰减,而呈现不断反弹,即自相关系数消退速度极慢,说明{xt}序列具有微弱但却长久的记忆。
二、ARCH-M(ARCH in mean模型)
Engle和Robins于1985提出的ARCH-M模型,是ARCH模型考虑到条件方差作为随时间改变的风险度量这一重要用途,而将风险与收益紧密联系在一起产生的。80年代初,以利率衡量的风险报酬受到重视的背景下,ARCH-M基于一种普遍投资心理“风险越大,期望的收益也越大;反之亦然。”而建立,是ARCH的拓展,使条件异方差直接影响收益的均值。

为增强概括能力,(4)、(5)式合并写作更一般的形式:
![]()
f()的具体形式表示收益与风险的比例关系,常设为线性。例如,两种资产:其一无风险,价格设定为1,弹性供给,收益为r;其一有风险,价格为p,随机收益为q,且![]() 则有:
则有:
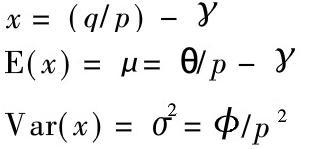
ARCH-M所表达的经济意义显著,但其局限性同LARCH模型。
三、TARCH(Threshold ARCH)
TARCH模型是一种考虑了![]() 与
与![]() 的符号有关的模型,其方差公式如下,其它与ARCH相同:
的符号有关的模型,其方差公式如下,其它与ARCH相同:
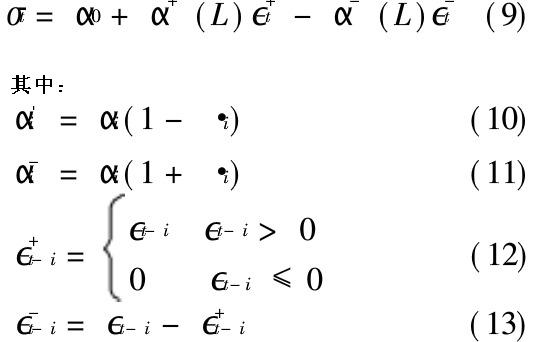
四、NARCH
NARCH是一种非线性ARCH,其方差公式如下,其它与ARCH相同:
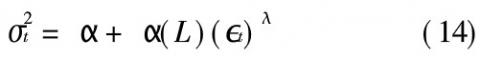
五、LGARCH模型
实际应用中对完全自由的滞后分布的估计导致对非负约束的破坏,且ARCH模型无法表述自相关系数消退很慢的某些情形。GARCH模型应运而生。其定义如下:
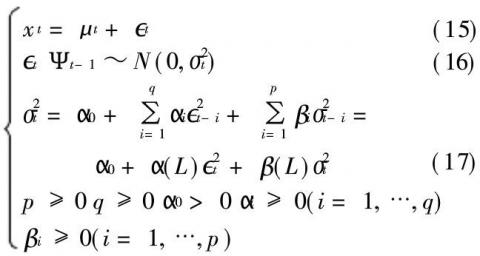 当p=0时,这就是ARCH(q)过程;当p=0时,{
当p=0时,这就是ARCH(q)过程;当p=0时,{
著作权归作者所有。商业转载请联系本站作者获得授权,非商业转载请注明出处 ZZKOOK。

评论
LZ实在最棒
我一定要加个标签收藏了
LZ实在好到没有朋友