一、离差
指单项数值和平均值的差,正负可以作为方向。用来反映某一数值与平均值的偏离程度(距离)。
二、标准差(sd)
用来反映样本数据离散程度的指标。多用来反映样本是否“稳重”。比如一学生整个学期的数学成绩作为样本,计算其标准差,标准差小代表该学生的成绩比较稳定。当然没有固定的标准,多用来比较多组数据的“靠谱性”。
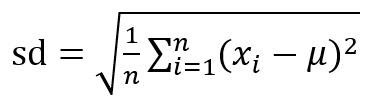
其中,n为样本的大小(样本自由度,样本频数),u为样本平均数。
三、方差
标准差平方后的值。一样的作用。
四、偏度
偏度反应分布的对称情况,。正态分布是完全对称的,所以正态分布的偏度为零。但是现实中很多分布是不对称的,有的偏向左边,有的偏向右边,所以就用偏度来衡量分布偏离的程度。
偏度是离群值(Outliers)导致的。离群值是那些正数中特别大或者负数中特别小的值,也就是绝对值特别大的值。从名字也可以看出来,这些数值特别不合群,不是特别大,就是特别小,有点离群索居的感觉,所以叫做离群值。
当离群值在正数中特别大的时候,分布就是右偏(Positively Skewed)的,在分布的右侧有一个长尾。对于右偏分布而言,平均值 > 中位数 > 众数。
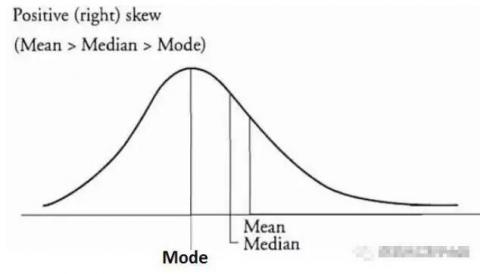
当离群值在负数中特别小的时候,分布就是左偏(Negatively Skewed)的,在分布的左侧有一个长尾。对于左偏分布而言,平均值 < 中位数 < 众数。
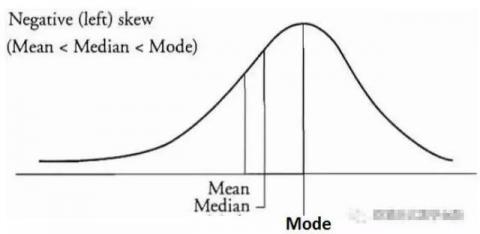
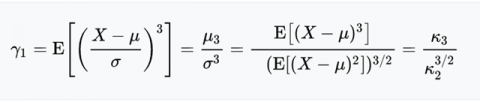 样本X的偏度为样本的三阶标准矩其中μ是均值,δ为标准差,E是均值操作,μ3是三阶中心距。
样本X的偏度为样本的三阶标准矩其中μ是均值,δ为标准差,E是均值操作,μ3是三阶中心距。五、峰度
峰度反应的是图像的尖锐程度:峰度越大,表现在图像上面是中心点越尖锐。在相同方差的情况下,中间一大部分的值方差都很小,为了达到和正太分布方差相同的目的,必须有一些值离中心点越远,所以这就是所说的“厚尾”,反应的是异常点增多这一现象。
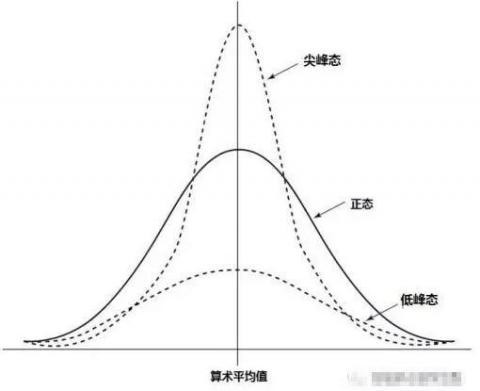
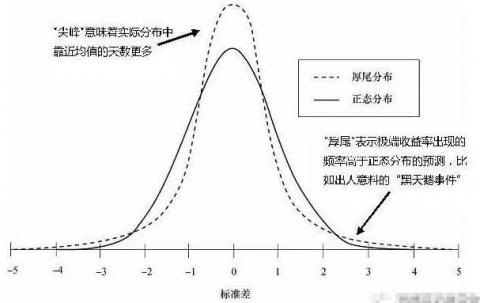
尖峰分布如果仅仅是尖峰就简单了,但是实际上,尖峰分布通常都会伴随着肥尾一同出现,即“尖峰肥尾”,或“尖峰厚尾”。从下图中可以看出,尖峰分布的峰(即平均值)和尾(即正负两端)都比正态分布的概率高,而在其他地方都比正态分布的概率低。
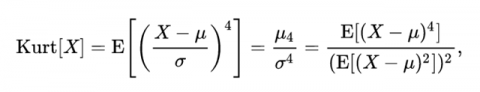
其中k4是四阶累积量的唯一对称无偏估计,k2是二阶累积量的无偏估计(等同于样本方差),m4是样本四阶平均距,m2是样本二阶平均距。
著作权归作者所有。商业转载请联系本站作者获得授权,非商业转载请注明出处 ZZKOOK。

评论
感谢
楼主是好人!
这是一条奉献的路,博主,坚持。
浮云游子意,落日猿友情。